
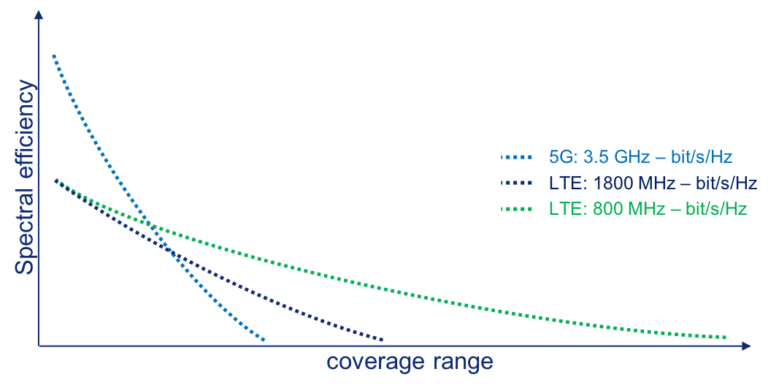
In other words, Massive MIMO means fewer dropped calls, a significant decrease in dead zones, and better quality data transmission, all without stretching the limits of our increasingly scarce radio spectrum.īetter still, Massive MIMO promises to reduce costs and improve energy efficiency compared with current LTE (4G) networks while providing reliability improvements through redundancy from the increased number of antennas. This means we can serve more users in a dense area without consuming any more radio spectrum or causing interference. Massive MIMO uses large numbers of antennas (more than 64) at a base station to spatially multiplex. While 4G networks theoretically support up to 10,000 active users per km², 5G should eventually support more than 1,000,000 active devices per km².Unlocking the potential of 5G networks starts with understanding the benefits of Massive MIMO. While 4G has a downlink spectral efficiency between 0.074 to 6.1 bits/s/Hz (bits per second per hertz), future 5G networks promise efficiencies of between 0.12 - 30 bits/s/Hz.Īs IoT devices become more prevalent, support for higher capacity is critical. Higher modulation schemes don’t just help individual users: they also increase the capacity of the network as a whole, bringing it closer to the Shannon Capacity. Along with beamforming, this should make higher quality signal levels and high-order modulation schemes much more common, increasing the data transmission rates between towers and users. Since 5G mmWave networks require the use of “small cells” covering smaller areas, interference between neighboring cells is dramatically decreased. These higher-order modulation schemes only become useful when signal quality is very high. We’ll cover how 5G networks improve latency in a future post. Latency, or the time it takes to reach a server, is not limited by Shannon’s Law and has a huge impact on everyday Internet usage. Please note, we’re completely ignoring latency here. To understand how 5G achieves these higher data rates, we need to dig into Shannon’s Law to see how engineers have tackled each of the limiting factors from previous generations. By this measure, at a minimum of 100 Mbps, 5G should be at least five times faster than average 4G speeds. The more useful metric defined by the International Telecommunications Union (ITU) for the IMT-2020 standard (basically the 5G standard) is user experience data rate, which is the data rate experienced by users in at least 95% of the locations where the network is deployed for at least 95% of the time.
#5g spectral efficiency android
You probably don’t see 1 Gbps download speeds on your LTE Android or iPhone handset. Theoretical peak rates are just that: theoretical. 5G takes that one step further next-generation networks will have peak theoretical data rates of 20 Gbps for downlink and 10 Gbps for uplink. 2G networks offered a maximum theoretical data rate of 40 kbps–but today’s 4G LTE-Advanced networks have peak theoretical data rates of 1 Gbps. Every successive cellular generation has brought dramatic increases in data rates. Combined with earlier work by Ralph Hartley, Shannon’s theorem sets an upper limit on the rate at which data can be transmitted over any communications channel, whether wired or wireless.Īs cellular communication has progressed in the last two decades, we’ve rapidly approached the theoretical limits for wireless data transmission set by Shannon’s Law. The theory sets an upper bound for the efficiency of the error-correction algorithms necessary when data is transmitted through a medium with noise (i.e. Shannon was a contemporary of Alan Turing and is considered by many to be the father of Information Theory.Īfter laying the foundation for much of modern cryptography during his work at Bell Labs during World War 2, Shannon developed his noisy channel coding theorem. Those limits have been known since the early 1950s as a result of the groundbreaking work by Claude Shannon.
Whether it’s over copper wire, through fiber-optic cables, or wirelessly, there are theoretical limits for each medium.


 0 kommentar(er)
0 kommentar(er)
